В преддверии лета всех интересует вопрос: повторится ли аномально жаркий период? Чтобы найти ответ на этот вопрос ученые из ряда стран используют различные математические модели, основываясь на данных погодных наблюдений в Европе за последние 510 лет.
Чтобы увидеть, насколько необычным был прошлый год с точки зрения статистики, посмотрим на карту ниже. На карте разными цветами показаны аномальные зоны температур летом 2010 года (красным – повышенная температура, синим – пониженная, белый соответствует средним показателям).

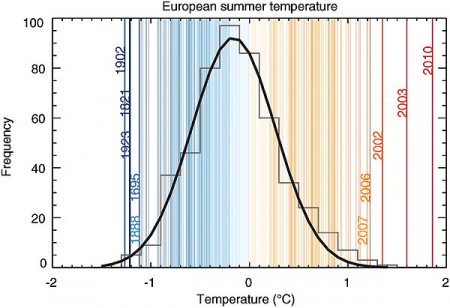
Еще более впечатляющим выглядит график частотного распределения летних температур в Европе за период с 1500-го по 2010 год . График выглядит как кривая Гаусса. Каждая вертикальная полоска – год.
Синие полоски слева демонстрируют аномально холодные года (самый холодный за последние 510 лет был 1902 год). Справа – аномально жаркие года. Но ряд линий явно выходят за хвосты «нормального распределения». Таким был 2003 год и, в особенности, 2010 год.
Остался открытым вопрос: когда может повториться небывалая летняя жара? Математические модели показывают, что жара как в августе 2003 года может повториться в течение 2020–2049 годов с частотой раз в 10 лет в Восточной Европе и раз в 15 лет — в Западной. События же лета 2010 года еще более маловероятны для первой половины XXI века. Однако к концу столетия повторения таких подъемов температур летом можно будет ожидать уже раз в 8 лет в Восточной Европе и раз в 4 года в Западной.
Впрочем, всецело полагаться в таком зыбком деле как прогнозы погоды на законы математики было бы наивно. В жизни не все можно перевести на язык цифр.
Есть замечательный анекдот на эту тему:
Математик и философ стоят на улице и смотрят на проходящих мимо людей. Философ спрашивает у математика: какова вероятность что мимо них подряд пройдут 5 людей одного пола? А 10 человек? А 100? И предлагает поспорить, что сейчас мимо них пройдет подряд 100 человек одного пола! Математик со смехом называет исчезающе малую вероятность такого явления и убеждает, что ждать такого события можно годами. И вот, пока наши герои стоят и разговаривают, мимо них проходит военный оркестр из 100 человек…
 3 098
3 098


